角点检测算法总结
0 引言
尽管进入了AI时代,特征点检测的传统算法日渐式微,但经典算法的原理和思维依旧值得学习和研究。网上对角点检测的介绍文章零零散散,鱼龙混杂。这说明要想专门研究某领域还是得阅读专业书或者学习靠谱的网课。
这里给想全面了解计算机视觉的推荐此书:Szeliski_Computer Vision Algorithms and Applications_2ndEd。本文部分内容会参考于此。
本文对经典的角点检测算法原理进行简要总结,包括Harris、FAST、Shi-Tomasi、AGAST、Phase Congruency、SuperPoint等,也含有一些不常见的角点算法(代数矩),和一些连接点检测算法(Pb)。SIFT、ORB等不在此列,前者不一定是角点,后者本质还是多尺度的FAST。
本文只涉及核心原理,较难理解处会尝试提供一些参考资料。本质是一篇信息整合,仅适合初学者阅读,用于对角点检测算法的快速了解,避免网上重复搜索。如有错误烦请指出。
本文首发于知乎平台:从Harris到SuperPoint: 一篇“简短”的角点检测算法总结
1 Moravec、Harris、Shi-Tomasi
1.1 Moravec
首先Moravec算法的原理很简单,邻域在四个方向的变化都比较大则邻域中心为角点。具体而言,考虑图像局部区域4个方向的SSD
\[\begin{aligned} V_{h}&=\sum_{i=-k}^{k-1}{(I_{x+i,y}-I_{x+i+1,y})^{2}} \\ V_{v}&=\sum_{i=-k}^{k-1}(I_{x,y+i}-I_{x,y+i+1})^{2} \\ V_{d}&=\sum_{i=-k}^{k-1}(I_{x+i,r+i}-I_{x+i+1,r+i+1})^{2} \\ V_{a}&=\sum_{i=-k}^{k-1}(I_{x+i,y-i}-I_{x+i+1,y-i-1})^{2} \end{aligned}\tag{1.0.1}\]然后将四个SSD的最小值作为中心像素的响应值
\[CRF(x,y)=\min\left\{V_{h},V_{v},V_{d},V_{a}\right\}\tag{1.0.2}\]1.2 Harris和Shi-Tomasi
Harris算法是对Moravec算法的改进1,其所用的自相关矩阵(auto-correlation matrix)最早于1981被Lucas、Kanade提出,后来也以类似原理提出光流(optical flow)。
特征点一般用于与另一张图进行匹配,但我们无法预先获知某一点用于匹配时的稳定性,但我们可以判断该点在小范围内的特异性,方法如下。
我们考虑图像 $I$ 以某一点 $\mathbf x_c$ 为中心的半径为 $m$ 的窗口 $W_m$ 下的邻域 \(\mathcal {N}\) ,窗口 \(W_m\) 发生一个微小的偏移 \(\Delta \mathbf u\) 后, \(W_m\) 下的另一邻域 \(\mathcal{N'}\) 与 \(\mathcal N\) 的差异。定义自相关函数(auto-correlation function)反映不同偏移下的邻域差异变化
\[E_{AC}(\mathbf x_c,\Delta \mathbf u)=\sum_i w(\mathbf{x}_{i})[I(\mathbf x_i+\Delta \mathbf u)-I(\mathbf x_i)]^2\tag{1.1}\]其中\(\mathbf x_i \in \mathcal N\), \(w(\mathbf{x}_{i})\) 是以 \(\mathbf x_c\) 为中心的权重函数,一般取高斯函数。注意其中 \(\mathbf x_c,\Delta \mathbf u\) 都是自变量,意味着 \(E_{AC}\) 在图像某一点 \(\mathbf x_c\) 固定时,不同的偏移 \(\Delta \mathbf u\) 有不同的值。严格来说它并不符合相关函数的定义,计算方式属于平方差求和(SSD)。
利用泰勒展开 \(I(\mathbf{x}_{i}+\Delta\mathbf{u})\approx I(\mathbf{x}_{i})+\nabla I(\mathbf{x}_{i})\cdot \Delta \mathbf u\) 代入公式 \((1.1)\) 中得到
\[\begin{aligned} E_{\mathrm{AC}}(\mathbf x_c,\Delta \mathbf u)& =\sum_{i}w(\mathbf{x}_{i})[I(\mathbf{x}_{i}+\Delta\mathbf{u})-I(\mathbf{x}_{i})]^{2} \\ &\approx\sum_{i}w(\mathbf{x}_{i})[I(\mathbf{x}_{i})+\nabla I(\mathbf{x}_{i})\cdot\Delta\mathbf{u}-I(\mathbf{x}_{i})]^{2} \\ &=\sum_{i}w(\mathbf{x}_{i})[\nabla I(\mathbf{x}_{i})\cdot\Delta\mathbf{u}]^{2} \\ &=\sum_{i}w(\mathbf{x}_{i})[ \Delta\mathbf{u}^T\nabla I(\mathbf{x}_{i})]^{2} \\ &=\sum_{i}w(\mathbf{x}_{i})\Delta\mathbf{u}^T[\nabla I(\mathbf{x}_{i})\nabla I(\mathbf{x}_{i})^{T}] \Delta\mathbf{u}\\ &=\Delta\mathbf{u}^T\Big\{\sum_{i}w(\mathbf{x}_{i})[\nabla I(\mathbf{x}_{i})\nabla I(\mathbf{x}_{i})^{T}] \Big\}\Delta\mathbf{u}\\ &=\Delta\mathbf{u}^{T}\mathbf{A}\Delta\mathbf{u} \end{aligned}\tag{1.2}\]其中, \(\mathbf{A}\) 被称作自相关矩阵或者结构张量。不难看出 \(\mathbf{A}\) 大小为2x2并可以写作:
\[\begin{aligned} \mathbf{A}&=\sum_{i}w(\mathbf{x}_{i})[\nabla I(\mathbf{x}_{i})\nabla I(\mathbf{x}_{i})^{T}]\\ &=\begin{bmatrix}\sum w(\mathbf{x}_{i})I_x(\mathbf{x}_{i})^2&\sum w(\mathbf{x}_{i})I_x(\mathbf{x}_{i})I_y(\mathbf{x}_{i})\\\sum w(\mathbf{x}_{i})I_x(\mathbf{x}_{i})I_y(\mathbf{x}_{i})&\sum w(\mathbf{x}_{i})I_y(\mathbf{x}_{i})^2\end{bmatrix}\\ &=w*\begin{bmatrix}I_x^2&&I_xI_y\\I_xI_y&&I_y^2\end{bmatrix} \end{aligned}\tag{1.3}\]最后一个等式的卷积也不符合严格意义上的常规卷积计算,可以理解成步幅 \(strides=m\)的卷积。 根据Moravec提出的角点定义,角点是在所有方向上灰度变化都很大的点,因此如果 \(\mathbf x_c\) 是角点,对应于 \(E_{AC}(\mathbf x_c,\Delta \mathbf u)\) 在 \(\mathbf x_c\)处无论 \(\Delta \mathbf u\) 取值多少都是一个较大的值。
网上很容易找到以下的描述,用 \(\mathbf{A}\) 的特征值 \(\lambda_{1,2},\lambda_1\geq\lambda_2\) 来判断\(\mathbf x_c\)的类型:
- 如果 \(\lambda_1\gg\lambda_2\) ,则 \(\mathbf x_c\)为边缘
- 如果 \(\lambda_1\approx\lambda_2\gg0\) ,则\(\mathbf x_c\)为角点
- 如果 \(\lambda_1\approx\lambda_2\approx0\) ,则\(\mathbf x_c\)为平坦区域
但是究竟是怎么从\(\mathbf{A}\)** 的特征值\(\lambda_1\approx\lambda_2\gg0\)推导出\(E_{AC}(\mathbf x_c,\Delta \mathbf u)\)在 \(\mathbf x_c\)处无论 \(\Delta \mathbf u\) 取值多少都是一个较大的值,所以** \(\mathbf x_c\)是角点这一结论的呢?
这里我们需要先明白两件事:
- 特征值和特征向量为满足等式 \(\mathbf A\mathbf x=\lambda \mathbf x\) 的 \(\lambda\) 和 \(\mathbf x\) ;
- 椭圆和矩阵的联系。中学学过椭圆方程为 \(\frac{x^2}{a^2}+\frac{y^2}{b^2}=1\) ,不难理解其可写成如下形式
不难求出 \(\mathbf B\) 的特征值为 \(\lambda_{2}=1/a^{2},\lambda_{1}=1/b^{2}\) ,特征向量为 \(\left. \mu_1=\left[\begin{array}{c}1\\0\end{array}\right.\right],\mu_2=\left[\begin{array}{c}0\\1\end{array}\right]\) ,椭圆的对称轴和特征向量平行,长轴等于更小的特征值的倒数平方,短轴等于更大的特征值的倒数平方。对于更一般的椭圆表达式 \((1.5)\) 一样有此结论2。
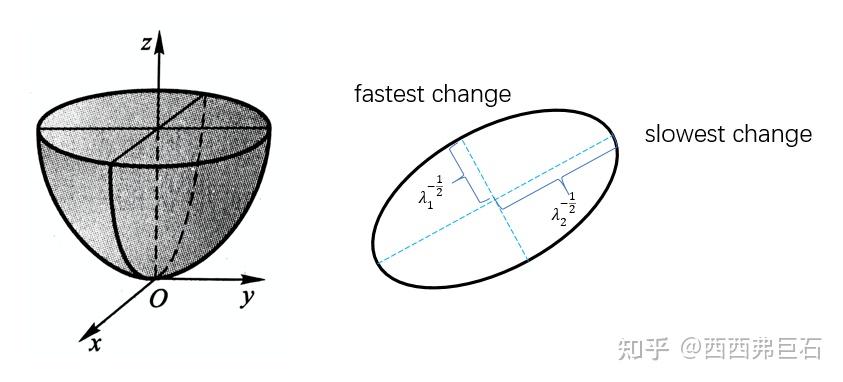
\[\begin{bmatrix}x\\y\end{bmatrix}^T\begin{bmatrix}a&b\\b&c\end{bmatrix}\begin{bmatrix}x\\y\end{bmatrix}=\mathbf x^T\mathbf A\mathbf x=1\tag{1.5}\]现在正式分析。自相关函数 \(E_{\mathrm{AC}}(\Delta\mathbf{u})=\Delta\mathbf{u}^{T}\mathbf{A}\Delta\mathbf{u}\) ,本质是一个 \((\Delta x,\Delta y,E)\) 坐标系下的椭圆锥面。
根据角点的自相关函数特征,角点处的 \(E_{\mathrm{AC}}\) 对所有 \(\Delta\mathbf{u}\) 都有一个较大的值,那么对应于椭圆锥面的形状就应该是比较“尖”和内缩的。不难想到其水平切面的轮廓是椭圆,形状就应该是比较小且接近于圆形,也即长轴和短轴都比较短且相近。我们考虑任意一处
\(E_{\mathrm{AC}}(\Delta\mathbf{u})=E_O\) 的切面椭圆,研究自相关矩阵 \(\mathbf{A}\) 对其形状的影响,其椭圆方程为 \(\frac{\Delta\mathbf{u}^{T}\mathbf{A}\Delta\mathbf{u}}{E_0}=1\tag{1.6}\)
\(\mathbf{A}\) 的特征值和特征向量可以反映这一椭圆的性质,我们可以对 \(\mathbf{A}\) 做特征值分解得到
\[\mathbf A=\mathbf R^{T} \mathbf\Lambda \mathbf R=\mathbf R^{T}\begin{bmatrix}\lambda_1&0\\0&\lambda_2\end{bmatrix}\mathbf R\tag{1.7}\]其中 \(\mathbf R=[\mathbf v_1,\mathbf v_2]\) 是一个正交矩阵,也可以看作一个旋转矩阵,看成一个变换就是 \(SO(2)\) 的元素。那么椭圆方程 \((1.6)\) 可以改写成
\[\frac{\Delta\mathbf{u}^{T}\mathbf R ^{T}\mathbf\Lambda \mathbf R\Delta\mathbf{u}}{E_0}=1\tag{1.8}\]其中 \(\Delta\mathbf{u}^{T}\mathbf R ^{T}\mathbf\Lambda \mathbf R\Delta\mathbf{u}=(\mathbf R^{T}\Delta \mathbf u^{T})^{T} \mathbf\Lambda \mathbf R\Delta\mathbf{u}\) 很显然可以看成对椭圆进行旋转,旋转矩阵为 \(\mathbf R\) ,椭圆的对称轴方向即为特征向量的方向。而 \(\Lambda\) 表明了椭圆的长短轴分别为 \(\frac{1}{\lambda_1^2E_0^2},\frac{1}{\lambda_2^2E_0^2}\) 。这两相近且都比较小时对应角点,这就得到了我们的结论: \(\lambda_1 \approx \lambda_2 \gg0\) 时对应于角点。
原论文将上述结论转换为一个单一的响应值
\[R(\mathbf x_c) = \text{det}(\mathbf{A})-\alpha\text{trace}(\mathbf{A})^2=\lambda_1\lambda_2-\alpha(\lambda_1+\lambda_2)^2\tag{1.9}\]后续对Harris算法的响应函数有很多的改进,比如Shi-Tomasi算法的响应函数为 \(R(\mathbf x_c)=\min(\lambda_1,\lambda_2)\) 。其余的一些响应值的改进包括: \(\lambda_{1}-\alpha\lambda_{2}\) 、 \(\frac{\lambda_{1}\lambda_{2}}{\lambda_{1}+\lambda_{2}}\) 。
1.# OpenCV API
1
2
void cv::cornerHarris( InputArray src, OutputArray dst, int blockSize, int ksize, double k, int borderType = BORDER_DEFAULT );
void cv::goodFeaturesToTrack( InputArray image, OutputArray corners, int maxCorners, double qualityLevel, double minDistance, InputArray mask = noArray(), int blockSize = 3, bool useHarrisDetector = false, double k = 0.04 );
展开
2 FAST
FAST算法全称是Features from Accelerated Segment Test,直译是加速分段测试特征。初始的FAST算法原理很简单,在论文中占幅不到一页3。
对于一个待测点 \(\mathbf x_c\) ,FAST考虑以 \(\mathbf x_c\) 为中心半径为3的 \(Bresenham\) 圆域 \(\mathcal C_{r=3}\) ,圆域 \(\mathcal C\) 共计16个像素,把这16个像素代表的方位用1~16的数字标识,记为 \(i\in \{1,2,...,16\}\) ,对应的像素记为 \(\mathbf x_i \in \{\mathbf x_1,\mathbf x_2,...,\mathbf x_{16}\}\) 。FAST提出的判准是:如果在圆域 \(\mathcal C\) 上存在连续 \(N\) 个和 \(\mathbf x_c\) 亮度差异较大的像素,则 \(\mathbf x_c\) 为角点。其中 \(N\) 一般取一个较大的数,比如9或12。而亮度差异则用阈值法衡量,对于圆域 \(\mathcal C\) 上的像素 \(\mathbf x_i\) ,如果其满足 \(\vert I(\mathbf x_i)-I(\mathbf x_c)\vert>t\) 则视为亮度差异较大, \(t\) 一般取20。
根据定义满足阈值条件的必需为连续像素,当 \(N=12\) 时,很显然有一种快速判断 \(\mathbf x_c\) 不是角点的方法(High-speed test): \(\{\mathbf x_1,\mathbf x_5,\mathbf x_9,\mathbf x_{13}\}\) 中如果存在3个像素不满足 \(\vert I(\mathbf x_i)-I(\mathbf x_c)\vert>t\) 则 \(\mathbf x_c\) 不是角点。
论文中指出,FAST计算十分迅速,但是明显存在这些问题:
- 当 \(N<12\) 时High-speed test就失效了;
- 特征的形状影响测试像素的选择和顺序;
- High-speed test的4个测试信息被丢弃了;
- 检测出的特征点很多彼此相邻。
于是,论文以此为基础进一步基于机器学习的方法提出了一个角点检测器。基本原理是根据特定的数据集训练一个决策树,这16个方位就是决策树的每个节点属性,从决策树训练的方式来决定这16个位置的使用,从而解决上述的前三个问题。至于第四个问题则通过极大值抑制来解决。
下面具体介绍训练的过程,为了尽量保证本文的符号一致,下面的记号与论文略有差异。
首先,根据应用场景,准备一个带有角点分类标签的图像数据集,即为所有训练图像的每一个像素赋予标签 \(Kp\in \{true,false\}\) 表示其是否为角点。
对于每一个中心像素 \(\mathbf x_c\) 和圆域 \(\mathcal C\) 上的一个方位 \(i\) ,我们以 \(t\) 和 \(-t\) 为界,记 \(\mathbf x_c \rightarrow i\) 为相对 \(\mathbf x_c\) 方位 \(i\) 处的像素, \(S_{\mathbf x_c \rightarrow i}\) 为根据 \(I(\mathbf x_i)-I(\mathbf x_c)\) 的取值划分的状态,也可以写作这两个变量的函数 \(S(\mathbf x_c , i)\) 。
\[\left.S_{\mathbf x_c \rightarrow i}=\left\{\begin{array}{ll}d,&\quad I_{\mathbf x_c\to i}\le I_{\mathbf x_c}-t&\text{(darker)}\\s,&\quad I_{\mathbf x_c}-t<I_{\mathbf x_c\to i}<I_{\mathbf x_c}+t&\text{(similar)}\\b,&\quad I_{\mathbf x_c}+t\le I_{\mathbf x_c\to i}&\text{(brighter)}\end{array}\right.\right.\tag{2.1}\]记所有训练图像的所有像素的集合为 \(P\) ,那么对于一个指定的方位 \(i\) ,我们都能根据公式 \((2.1)\) 将 \(P\) 分为三个子集 \(P_d,P_s,P_b\) 。
然后根据ID3算法4最大化信息增益(Infomation Gain)5生成决策树,也即决策树的每个节点都选择信息增益最大的方位 \(i_m\) 作为属性,然后以 \(i_m\) 为参数将输入集继续分为三个子集,接着对子集循环执行上述操作,找信息增益最大的方位 \(i_m'\) (可以与 \(i_m\) 相同)、拆分子集……直到子集的熵为零操作终止,此时所有子集的像素均为同类别,即都为角点或非角点,至此完成决策树的生成。
| 这里的信息增益 \(H_g(P)\) 算法如下,首先 \(P\) 是一个以是非角点划分的二类别像素集,记 $$c=\vert {p | K_{p} = \mathrm{true}}\vert\(为角点的总数,\)\bar{c}=\vert {p | K_{p}=\mathrm{false}}\vert\(为非角点的总数,那么\)P$$ 的信息熵为 |
\(H(P)=(c+\bar{c})\log_2(c+\bar{c})-c\log_2c-\bar{c}\log_2\bar{c}\tag{2.2}\) 这是论文中的写法,乍一看不符合信息熵的公式,稍作变换即可写成频率的形式 \(H(P)=-c\log_2\frac{c}{c+\bar c}-\bar{c}\log_2\frac{\bar c}{c+\bar c}\tag{2.3}\)
这样一看严格而言 \(H(P)\) 还要除以 \(c+\bar c\) 才是真正的信息熵。接下来的信息增益表达的是 \(P\) 和在某一属性划分之下的子集之间的信息差异,论文中的公式为
\[H_g(P)=H(P)-H(P_d)-H(P_s)-H(P_b)\tag{2.4}\]但从信息增益的定义出发,其公式应写为 \(H_g(P)=IG(P,i)=H(P)-\sum_{S_{\mathbf x_c \rightarrow i}\in\{d,s,b\}}\frac{\vert P_{S_{\mathbf x_c \rightarrow i}}\vert}{\vert P\vert}H\left(P_{S_{\mathbf x_c \rightarrow i}}\right)\tag{2.5}\) 也即后面三项有一个表示子集元素数量占比的系数,求和项应为 \(P_{S_{\mathbf x_c \rightarrow i}}\) 的数学期望。
2.# OpenCV API
1
void cv::FAST(InputArray image, std::vector<KeyPoint> &keypoints, int threshold, bool nonmaxSuppression = true);
展开
3 AGAST
AGAST算法的原理介绍文章在互联网上几乎没有,很多都只是一笔带过直接摆出OpenCV接口。
于是我选择直接阅读AGAST论文6。尽管介绍核心原理的部分也比较简短,但我还是研究了好几天,以下是个人理解:
首先,AGAST(Adaptive and Generic Accelerated Segment Test)算法是FAST算法的改进,全称为自适应和普适性的加速分段测试。AGAST算法与FAST算法都基于AST的判准,差异只在于决策树的构建上,不同于FAST需要针对应用场景来选择数据集进行训练,AGAST能够用预先构建好的2棵及以上的决策树对任意场景检测。
那AGAST是如何预先构建决策树呢?
首先,它将FAST中的三叉树改成了二叉树。
FAST在决策树的每一个节点都需要问 \(Q_1:I(\mathbf x_i)-I(\mathbf x_c)>t\) 和 \(Q_2:I(\mathbf x_i)-I(\mathbf x_c)<-t\) 两个问题,来为该节点赋予 \(\{d,s,b\}\) 三种状态之一。我们把从决策树的根节点到叶节点的所有节点属性 \(S_{\mathbf x_c \rightarrow i}\) 的组合 \(C_{S_{\mathbf x_c \rightarrow i}}=(C_{S_{\mathbf x_c \rightarrow 1}},C_{S_{\mathbf x_c \rightarrow 2}},...,C_{S_{\mathbf x_c \rightarrow N}})\) ,并且增添一个状态 \(u\) 代表该方位 \(i_u\) 的状态未知,其中某个确定的组合 \(C_{S_{\mathbf x_c \rightarrow i}}\) 我们称之为一个像素配置(pixel configuration),那么组合 \(C_{S_{\mathbf x_c \rightarrow i}}\) 共有 \(4^N\) 种可能,也即配置空间的大小为 \(4^N\) 。
由于FAST需要问两个问题因此会产生三个子节点,要生成二叉树每个节点只能问一个问题。AGAST算法在每个节点只选择 \(Q_1\) 或者 \(Q_2\) 判断子节点的输入,子节点的问题又会由父节点所决定。很显然在\(Q_1\) 或者 \(Q_2\) 不满足时需要引入新的状态来标记,文中使用 \(\bar{b}\) 和 \(\bar{d}\) 表示相应的:非更亮和非更暗的状态,公式上表达如下:
\[S_{\mathbf x_c\to i}=\begin{cases}d,&I_{\mathbf x_c\to i}<I_{\mathbf x_c}-t&\text{(darker)}\\\overline{d},&I_{\mathbf x_c\to i}\not<I_{\mathbf x_c}-t&\text{(not darker)}\\s,&I_{\mathbf x_c\to i}\not<I_{\mathbf x_c}-t\land S'_{\mathbf x_c\to i}=\overline{b}&\text{(similar)}\\s,&I_{\mathbf x_c\to i}\not>I_{\mathbf x_c}+t\land S'_{\mathbf x_c\to i}=\overline{d}&\text{(similar)}\\\overline{b},&I_{\mathbf x_c\to i}\not>I_{\mathbf x_c}+t\land S'_{\mathbf x_c\to i}=u&\text{(not brighter)}\\b,&I_{\mathbf x_c\to i}>I_{\mathbf x_c}+t&\text{(brighter)}\end{cases}\tag{3.1}\]其中 \(S'_{\mathbf x_c\to i}\) 表示父节点的状态, \(\land\) 表示逻辑与。从公式来看, \(d\) 和 \(b\) 的判别与FAST一致,但当某个节点判别为 \(\bar{b},\bar{d},u\) 时,需要在子节点选择对应问题对同一方位 \(i'\) 继续判断。比如当某一节点判断 \(Q_1\) 不满足时,标记其状态为非更亮 \(\bar{b}\) ,然后在子节点选择问题 \(Q_2\) 进一步判断, \(Q_2\) 判准满足则为更暗 \(d\) ,否则就标记为相似 \(s\) 。其余两种情况类似,本质就是将FAST在同一节点问两个问题改成了在相继的节点问互斥的问题,从而实现二叉树变为三叉树。
在这样的修改过后,状态由原来的4种变为6种,配置空间大小由 \(4^N\) 变为 \(6^N\) 。接下来构建最优二叉决策树,不同于FAST的ID3算法,AGAST使用了类似逆向归纳(Backward Induction)的方法,从叶节点开始逆向使得每一层的代价最小。论文中考虑以下三类计算损失:
- \(c_R\) :判断同像素方位两次的计算代价(register access cost)
- \(c_C\) :判断同行像素的计算代价(cache access cost)
- \(c_M\):判断任意其它像素的计算代价(testing of any other pixel)
首先根据深度优先搜索构建所有可能的配置空间,然后令所有的叶节点代价为零,逆向考虑逐层的代价使之最小来构建最优决策树。其中每一个节点的代价 \(c_P\) 根据两个子节点的代价 \(c_+,c_-\) 优化:
\[c_P=\min_{\{(C_+,C_-)\}}c_{C_+}+p_{C_+}c_T+c_{C_-}+p_{C_-}c_T=c_{C_+}+c_{C_-}+p_Pc_T\tag{3.2}\]其中 \(c_T\in\{c_R,c_C,c_M\}\) 是三种类型的计算代价之一, \(p_P\) 和 \(p_{c_+},p_{c_-}\) 分别是父节点和子节点的像素配置的概率,也即涌入元素在总训练数据的占比。这样我们就能得到最优的决策树。
接下来就是AGAST算法的核心部分,也即使其产生自适应和普适性的部分:使用多棵决策树跳转/拼接。
我们可以注意到FAST算法不具有旋转不变性,在训练数据旋转一定的角度后,相应的像素配置也得选择对应的角度。决策树学习的只是像素配置的概率分布,而不是训练图像的像素特性(平坦性的/纹理性的)的概率分布。那这两者之间有没有关联呢?
假设 \(p_s\) 为平坦性的像素的概率, \(p_t\) 为纹理性/结构性的像素的概率分布。观察到一个事实,当某一个像素相对某一个方位有较大的亮度偏差而标记为 \(b\) 或 \(d\) 时,比如 \(S_{\mathbf x_c\to 1}=b\) 时,那么镜像地考虑该方位对应的像素为中心时的状态就是反向的状态,也即 \(S_{\mathbf x_1\to 9}=d\) ,所以我们可以得到 \(p_t=2p_{bd}=p_b+p_d\) ,其中 \(p_{bd}\) 表示状态为 \(b\) 或 \(d\) 的像素的概率。
那么我们就可以得到像素配置的概率和像素分布的概率的关系:
\[p_X=\prod\limits_{i=1}^Np_i\quad\text{with}\quad p_i=\begin{cases}1&\text{for}&S_{\mathbf{x_c}\to i}=u\\p_s&\text{for}&S_{\mathbf{x_c}\to i}=s\\p_{bd}&\text{for}&S_{\mathbf{x_c}\to i}=d\lor S_{\mathbf{x_c}\to i}=b\\p_{bd}+p_s&\text{for}&S_{\mathbf{x_c}\to i}=\overline{d}\lor S_{\mathbf{x_c}\to i}=\overline{b}\end{cases}\tag{3.3}\]其中, \(\lor\) 表示逻辑或。不难看出 \(p_{X}\) 是子概率为 \({p_s,p_b,p_d}\) 的三项分布。
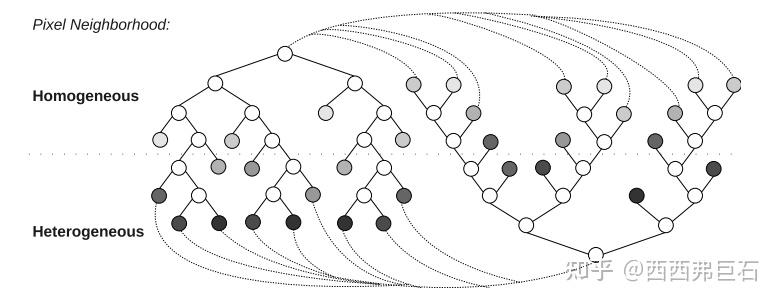
为了适应不同的应用场景,我们可以选择不同类型的数据集训练得到不同的决策树,比如分别用 \(p_s\) 比较小的结构性强的图像数据和 \(p_s\) 比较大的结构性弱的图像数据得到两棵决策树。在具体应用中,利用决策树判断像素类型时,其中一棵决策树到达叶节点后即刻跳转至另一棵决策树的根节点继续判断,由此来实现算法的自适应性,如图3.1所示。
图中节点颜色越浅表示涌入元素的异质性越强。
3.# OpenCV API
1
void cv::AGAST(InputArray image,std::vector<KeyPoint> &keypoints, int threshold, bool nonmaxSuppression, int type)
展开
4 Phase Congruency
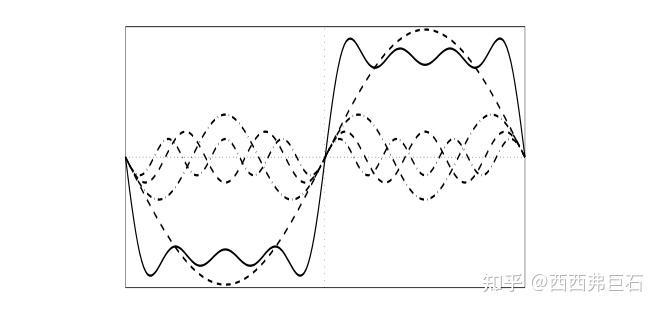
相位一致性(Phase Congruency)的核心思想在于如下观察:信号在跳变处的各个傅里叶分量相位相近。
相位一致性也可以理解成,对于一组傅里叶变换后的正弦波,如果在零点(对称中心)处有着越多的同向幅值叠加,会导致这个点的对比度(梯度)越大7。为什么说零点?因为正弦波的零点处的梯度最大。
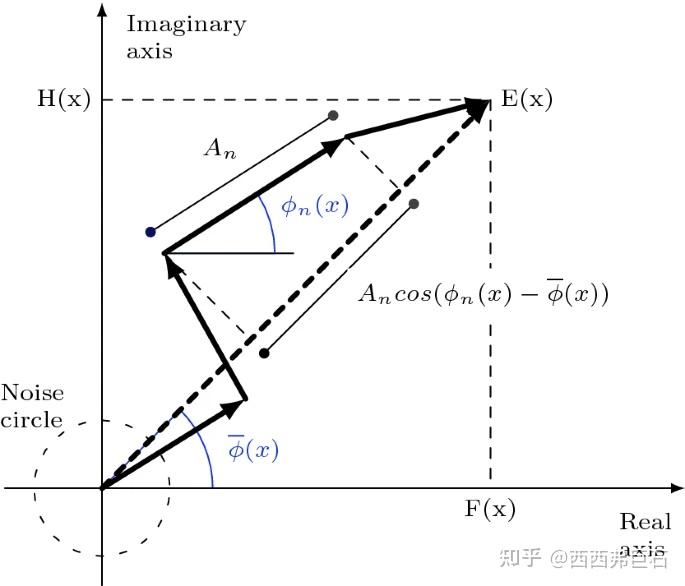
最初的的相位一致性公式为 \((4.1)\) ,式中 \(\vert E(x)\vert\) 是局部能量(Local Energy), \(A_n(x)\) 是各个傅里叶分量的幅值, \(\overline{\phi}(x)\) 是加权相位均值,也即“总相位”。
\[\begin{aligned} PC_1(x)&=\frac{|E(x)|}{\sum_nA_n(x)}\\ &=\frac{\sum_nA_n(\cos(\phi(x)-\overline{\phi}(x))}{\sum_nA_n(x)} \end{aligned}\tag{4.1}\]很显然, \(PC_1(x)\in [0,1]\) ,值越大对应于相位一致性越强。为了更好地定位特征并减弱噪声的影响,Kovesi8对相位一致性的公式进行了改良
\[PC_{2}(x)=\frac{\sum_{n}W(x)\lfloor A_{n}(x)(\cos(\phi_{n}(x)-\overline{\phi}(x))-|\sin(\phi_{n}(x)-\overline{\phi}(x))|)-T\rfloor}{\sum_{n}A_{n}(x)+\varepsilon}\tag{4.2}\]公式 \((4.2)\) 中, \(W(x)\) 是空域上的权重函数,对应点的频域范围越大权重越大。 \(\lfloor x\rfloor=\max(0,x)\) 表示非负函数,有点像DL中的ReLu激活函数, \(\varepsilon\) 是防止分母为零的极小量,阈值 \(T\) 用来过滤噪声的影响。
相位一致性的计算公式也可以写为9
\[PC(x)=\frac{\sum_nW(x)\lfloor A_n(x)\Delta\Phi_n(x)-T\rfloor}{\sum_nA_n(x)+\epsilon}\tag{4.3}\]其中的核心即局部能量函数的计算利用了log-gabor滤波器,局部能量各个傅里叶尺度下的分量计算方式为
\[\begin{aligned}A_n(x)\Delta\Phi_n(x)=A_n(x)(\cos(\phi_n(x)-\overline{\phi}(x))-|\sin(\phi_n(x)-\overline{\phi}(x))|)\\=(e_n(x)\cdot \overline{\phi}_e(x)+o_n(x)\cdot\overline{\phi}_o(x))-|e_n(x)\cdot\overline{\phi}_o(x)-o_n(x)\cdot\overline{\phi}_e(x)|\end{aligned}\tag{4.4}\]其中:
\[[e_n(x),o_n(x)]=[I(x)*M_n^e,I(x)*M_n^o]\tag{4.5}\]\(M_n^e\) 表示偶对称滤波(余弦波), \(M_n^o\) 表示奇对称波(正弦波),后者是前者的希尔伯特变换。而滤波结果的两个分量就对应于相应滤波尺度下的虚数形式,也即幅值 \(A_{n}(x)=\sqrt{e_{n}(x)^{2}+o_{n}(x)^{2}}\) ,相位 \(\phi_{n}(x)=atan2(e_{n}(x),o_{n}(x))\) 。而 \([\overline{\phi}_e(x),\overline{\phi}_o(x)]=\sigma'[\sum_n e_n(x),\sum_n o_n(x)]\) 表示加权相位角对应的单位向量, \(\sigma'\) 是归一化系数。
在实际计算中,由 \(I(x)\) 的频域经由log-gabor滤波后再逆变换回空域的实部和虚部就分别对应于 \(e_n(x)\) 和 \(o_n(x)\) 。log-gabor滤波本身具有多尺度和多方向的特性,后文的尺度 \(s\) 和角度 \(\theta\) 源自于此。log-gabor滤波只能用于频域,其可以表达为径向分量和角度分量的乘积
\[G(f,\theta)=G_r\cdot G_\theta = \exp\left(\frac{-(\log(f/f_0))^2}{2(\log(\sigma_f/f_0))^2}\right)\exp\left(\frac{-(\theta-\theta_0)^2}{2\sigma_\theta^2}\right)\tag{4.6}\]其中, \(f_0\) 和 \(\theta_0\) 分别表示中心频率和中心方向, \(\sigma_f\) 和 \(\sigma_\theta\) 分别控制频率带宽和角度带宽。一般通过设置最小波长、乘积因子和尺度数来实现滤波器的多尺度。
最后权重 \(W(x)\) 求法如下
\[W(x)=\bigg\{\exp \big[g\cdot\big( -\frac{\sum_n A_n}{s\cdot(\max A_n+\epsilon)}+c\big)\big]+1\bigg\}^{-1}\tag{4.7}\]式中 \(s\) 是所考虑的所有尺度数, \(c\) 是滤波器响应扩散的截止值,低于该值的将受到惩罚, \(g\) 是控制截止值锐度的增益因子。
针对图像这样的2D信号,我们实际提取出的相位一致性是带方向的 \(PC(x,\theta)\) ,论文中利用经典矩分析方程:
\[\begin{aligned} &a=\sum_\theta(PC(\theta)\cos(\theta))^{2} \\ &\begin{aligned}b=2\sum_\theta(PC(\theta)\cos(\theta))\cdot(PC(\theta)\sin(\theta))\end{aligned} \\ &c=\sum_\theta(PC(\theta)\sin(\theta))^{2} \end{aligned}\tag{4.8}\]然后我们就可以得到主轴: \(\Phi=\frac{1}{2}\arctan2\left(\frac{b}{\sqrt{b^2+(a-c)^2}},\frac{a-c}{\sqrt{b^2+(a-c)^2}}\right)\tag{4.9}\)
接着得到最小矩和最大矩,也分别对应于边缘特征和角点特征,也即 \(M\) 和 \(m\) 中值越大的位置分别就对应于边缘和角点。
\[\begin{gathered} M =\frac12(c+a+\sqrt{b^2+(a-c)^2}) \\ m =\frac{1}{2}(c+a-\sqrt{b^2+(a-c)^2}) \end{gathered}\tag{4.10}\]4.# C++ code
code:10
其中的log-gabor滤波的处理与公式 \((4.6)\) 存在细微的差异,角度分量用的是余弦函数而非高斯函数。
5 CSS、CPDA
这一类的算法都是基于以下的角点定义:角点是曲线上曲率最大的点。为了进一步约束一般加入以下条件:
- 曲率大于一定阈值或比局部最小曲率大 \(a\) 倍
- 多尺度检测
- 单独处理曲线交叉产生的连接点(junctions)
对于一条以参数方程形式表达的平面曲线:
\[\boldsymbol{r}(u)=(x(u),y(u))\tag{5.1}\]\([0,u]\)的弧长可以定义为:
\[s=\int_0^u|\dot{\boldsymbol{r}}(v)|dv\tag{5.2}\]那么,在 \(u\) 处的切向和法向单位向量分别为:
\[\begin{gathered} \boldsymbol{t}(u)=\frac{\dot{\boldsymbol{r}}}{|\dot{\boldsymbol{r}}|}=\left(\frac{\dot{x}}{\left(\dot{x}^{2}+\dot{y}^{2}\right)^{1/2}},\frac{\dot{y}}{\left(\dot{x}^{2}+\dot{y}^{2}\right)^{1/2}}\right) \\ \boldsymbol{n}(u)=\boldsymbol{t}^\perp(u)=\left(\frac{-\dot{y}}{(\dot{x}^{2}+\dot{y}^{2})^{1/2}},\frac{\dot{x}}{(\dot{x}^{2}+\dot{y}^{2})^{1/2}}\right) \end{gathered}\tag{5.3}\]根据 \(Serret-Frenet\) 向量等式可以得到:
\[\begin{aligned}\dot{\boldsymbol{t}}(s)&=\kappa(s)\boldsymbol{n}(s) \\ \dot{\boldsymbol{n}}(s)&=-\kappa(s)\boldsymbol{t}(s)\end{aligned}\tag{5.4}\]接下来可以考虑曲率了,其定义为:
\[\kappa(s)=\lim_{h\to0}|\frac{\phi}{h}|\tag{5.5}\]其中 \(\phi\) 是从 \(\boldsymbol{t}(s)\) 到 \(\boldsymbol{t}(s+h)\) 的角度。注意到:
\[\dot{\boldsymbol{t}}(s)=\frac{d\boldsymbol{t}}{ds}=\frac{d\boldsymbol{t}}{du}\frac{du}{ds}\tag{5.6}\]那么就有,
\[\dot{\boldsymbol{t}}(u)=\frac{d\boldsymbol{t}}{du}=\frac{ds}{du}\kappa \boldsymbol n=|\dot{\boldsymbol r}|\kappa\boldsymbol{n}\tag{5.7}\]这样我们就得到了曲率计算公式:
\[\kappa(u)=\frac{\langle\dot{\boldsymbol t},\boldsymbol n\rangle}{|\dot{\boldsymbol r}|}=\frac{\dot{x}(u)\ddot{y}(u)-\dot{y}(u)\ddot{x}(u)}{\left(\dot{x}(u)^{2}+\dot{y}(u)^{2}\right)^{3/2}}\tag{5.8}\]当然直接从定义 \((4.5)\) 出发,我们也可以得到另一种推导方式:
\[\begin{aligned} \kappa(u)&=|\frac{d\phi(t)}{ds(t)}|=\frac{1}{||ds||}\cdot d(\arctan{\frac{\dot{y}}{\dot{x}}})\\&=\frac{1}{(\dot{x}^{2}+\dot{y}^{2})^{1/2}\cdot dt}\cdot\frac1{1+[\dot y/\dot x]^2}\cdot\frac{\ddot y\dot x-\ddot x\dot y}{\dot x^2}\cdot dt\\ &=\frac{\ddot y\dot x-\ddot x\dot y}{(\dot{x}^{2}+\dot{y}^{2})^{3/2}} \end{aligned}\tag{5.9}\]在上述推导中参数 \(u\) 意义模糊,下面我们定义其为归一化弧长,并且引入高斯函数卷积得到如下的曲线集合:
\[\Gamma_{\sigma}=\{(X(u,\sigma),Y(u,\sigma))|u\in[0,1]\}\tag{5.10}\]其中的 \(\sigma\) 即为尺度因子。 \(X\) , \(Y\) 分别为:
\[\begin{aligned}X(u,\sigma)&=x(u)\otimes g(u,\sigma)\\ Y(u,\sigma)&=y(u)\otimes g(u,\sigma)\\ g(u,\sigma)&=\frac{1}{\sigma\sqrt{2\pi}}e^{\frac{-u^{2}}{2\sigma^{2}}}\end{aligned}\tag{5.11}\]对应的曲率为:
\[\kappa(u,\sigma)=\frac{X_{u}(u,\sigma)Y_{uu}(u,\sigma)-X_{uu}(u,\sigma)Y_{u}(u,\sigma)}{(X_{u}(u,\sigma)^{2}+Y_{u}(u,\sigma)^{2})^{3/2}}\tag{5.12}\]其中,
\[\begin{aligned} X_{u}(u,\sigma)&=\frac{\partial}{\partial u}(x(u){\otimes}g(u,\sigma))=x(u){\otimes}g_{u}(u,\sigma) \\ X_{uu}(u,\sigma) &=\frac{\partial^{2}}{\partial u^{2}}(x(u)\otimes g(u,\sigma)) =x(u)\otimes g_{uu}(u,\sigma) \\ Y_{u}(u,\sigma) &=y(u)\otimes g_{u}(u,\sigma) \\ Y_{uu}(u,\sigma) &=y(u)\otimes g_{uu}(u,\sigma) \end{aligned}\tag{5.13}\]CSS算法流程11
- 使用Canny算子提取边缘
- 提取轮廓并且对轮廓预处理:①填补边缘之间的间隙;②找到T型角点并标记
- 在最大的尺度计算曲率并根据阈值和邻域最小值得到候选点
- 在小尺度中进行角点跟踪
- 后处理:融合T型点,移除过于接近的两个角点中的一个
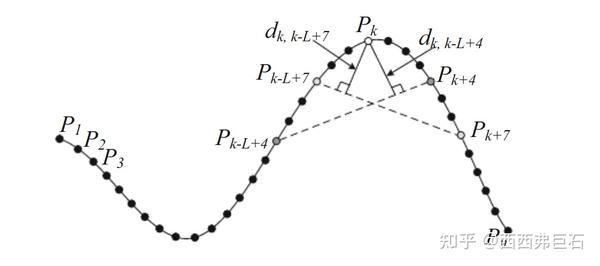
CPDA12的算法流程与CSS相近,不同的只有曲率的计算公式,不同于公式 \((5.12)\) ,CPDA用的的累计点弦距。计算方式即是给定一个弦长(或者给定弦长的x方向投影长),将这条弦从以右端和待测点重合开始,一直向右滑动直到左端与待测点重合,计算滑动过程中弦对应弧线上的点到弦的垂直距离之和,如图5.1所示。
5.# MATLAB code
CSS:13
CPDA:14
6 Algebraic Moments
6.1 角点模型
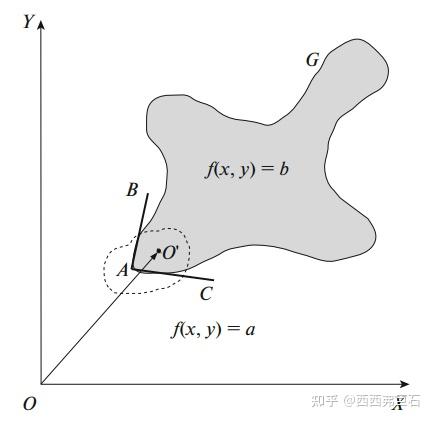
如图6.1所示, \(A\) 点即为待研究的角点,在局部区域可以视为一个 \(L\) 型角点, \(O^\prime\) 为角点邻近区域的一个点, \(AB\) 、 \(AC\) 为与与角点 \(A\) 关联的两条边。为了进一步简化模型,考虑以下灰度分布:即在 \(AB\) 、 \(AC\) 两侧的灰度值 \(f(x,y)\) 分别为 \(a\) 、 \(b\) 。
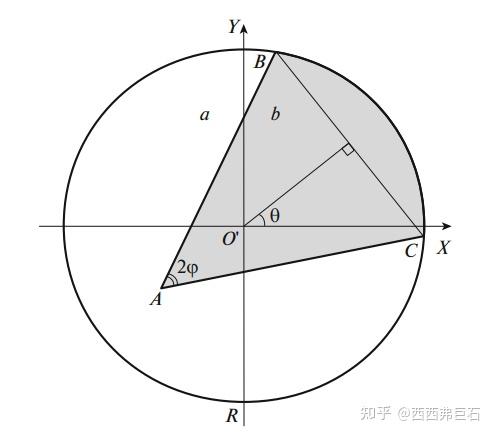
接下来考虑以 \(O^\prime\) 为中心的角点区域,如图6.2所示,该圆形区域半径为 \(R\) 。
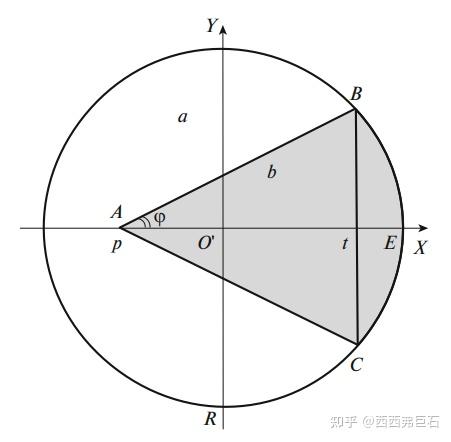
为了便于后续计算和分析,将图6.2中的坐标系逆时针旋转 \(\theta\) 角如图6.3所示。
在图6.3中, \(p\) 和 \(t\) 分别是 \(A\) 和 \(BC\) 的 \(X\) 坐标,其中满足 \(AB=AC\) ,整个半径为 \(R\) 的区域记为 \(S\) 。
6.2 代数矩分析
a.代数矩定义 在图6.2中的坐标系下, \(p+q\) 阶矩可以表示为:
\[m_{pq}=\iint\limits_Sx^py^qf(x,y)dxdy\tag{6.1}\]对于旋转了 \(\theta\) 角的图6.3,代数矩可以表示为:
\[\begin{aligned}M_{pq}=&\sum_{i=0}^{p}\sum_{j=0}^{q}\binom{p}{i}\binom{q}{j}(-1)^{q-j}\cos^{p-i+j}\theta\\&\times\sin^{q+i-j}\theta m_{p+q-i-j,i+j}\end{aligned}\tag{6.2}\]从图6.3中不难看出: \(M_{01}=\iint\limits_Syf(x,y)dxdy=0\) ,代入公式 \((6.2)\) 可得:
\[\begin{aligned}\cos\theta&=\frac{m_{10}}{\sqrt{m_{01}^2+m_{10}^2}}\\\\\sin\theta&=\frac{m_{01}}{\sqrt{m_{01}^2+m_{10}^2}}\end{aligned}\tag{6.3}\]据公式 \((2.3)\) 可以反解出角 \(\theta\) :
\[0=\begin{cases}0\quad\text{(by definition),}\quad\text{for}\quad m_{10}=0,\quad\text{and}\quad m_{01}=0,\\\frac{\pi}{2}\cdot sgn(m_{01}),\quad\text{for}\quad m_{10}=0,\quad\text{and}\quad m_{01}\neq0,\\\pi+\arctan\frac{m_{01}}{m_{10}},\quad\text{for}\quad m_{10}<0,\quad\text{and}\quad m_{01}>0,\\-\pi+\arctan\frac{m_{01}}{m_{10}},\quad\text{for}\quad m_{10}<0,\quad\text{and}\quad m_{01}<0,\\\arctan\frac{m_{01}}{m_{10}},\quad\text{otherwise}&\end{cases}\tag{6.4}\]其中符号函数 \(sgn(x)\) 定义为: \(sgn(x)=\begin{cases}-1,&\text{for}\quad x<0,\\1,&\text{for}\quad x\geq0\end{cases}\) 。
将公式 \((6.3)\) 代入公式 \((6.2)\) 可以得到两个坐标系下的代数矩的关系:
\[\begin{aligned}M_{pq}&=(m_{01}^2+m_{10}^2)^{-\frac{p+q}{2}}\sum_{i=0}^p\sum_{j=0}^q\binom{p}{i}\binom{q}{j}(-1)^{q-j}\\&\times m_{10}^{p-i+j}m_{01}^{q+i-j}m_{p+q-i-j,i+j}\end{aligned}\tag{6.5}\]b.参数求解 接下思考如何根据代数矩计算出四个参数 \(a,b,p,t\) 。其中 \(p\) 即为我们所需要的角点亚像素坐标。 首先,不难得到图6.3中的两条角点边线的代数表达式为,这将辅助后续的计算。
\[\begin{gathered} l_{AB}:y_{1}(x)=\frac{\sqrt{R^{2}-t^{2}}}{t-p}(x-p), \\ l_{AC}:y_{2}(x)=-{\frac{\sqrt{R^{2}-t^{2}}}{t-p}}(x-p). \end{gathered}\tag{6.6}\]接下来具体计算各阶代数矩的值:
\[\begin{aligned} M_{00}&=\iint_Sf(x,y)dxdy\\ &=a\iint_{S}dxdy+(b-a)\iint_{S_{ABC}}dxdy+(b-a)\iint_{S_{CBE}}dxdy \\ &=(a+b)\frac{\pi R^{2}}{2}+(a-b)\biggl(p\sqrt{R^{2}-t^{2}}+R^{2}\arcsin\frac{t}{R}\biggr) \end{aligned}\tag{6.7}\]其中 \(S_{ABC}\) 和 \(S_{CBE}\) 分别为图6.3中灰度值为 \(b\) 的三角形区域和弓形区域。类似地,可以计算得到:
\[\begin{aligned} M_{10}&=-\frac{a-b}{3}\sqrt{R^{2}-t^{2}}(2R^{2}-pt-p^{2}), \\ M_{20}&=\frac{a+b}2\frac{\pi R^{4}}4 \\ &-(a-b)\Biggl[\frac{1}{6}\sqrt{R^{2}-t^{2}}\left(\frac{3}{2}R^{2}t-pt^{2}-tp^{2}-p^{3}\right) \\ &-\left.\frac{R^{4}}{4}\arcsin\frac{t}{R}\right], \\ M_{02}&=\frac{a+b}2\frac{\pi R^{4}}4 \\ &-(a-b)\biggl[\frac{1}{6}\sqrt{R^{2}-t^{2}}\biggl(pt^{2}-R^{2}p-\frac{3}{2}R^{2}t\biggr) \\ &-\left.\frac{R^{4}}{4}\arcsin\frac{t}{R}\right] \end{aligned}\tag{6.8}\]观察公式 \((6.7)\) 和公式 \((6.8)\) 的各阶代数矩, \(M_{02}\) 和 \(M_{20}\) 分别减去 \(\frac{R^2}{4}M_{00}\) 可以消去第一项,那么可以得到:
\[\begin{aligned} H&=4M_{20}-R^{2}M_{00}=-4(a-b)\sqrt{R^{2}-t^{2}} \\ &{\times} \biggl[\frac{1}{6}\biggl(\frac{3}{2}R^{2}t-pt^{2}-tp^{2}-p^{3}\biggr)+\frac{1}{4}R^{2}p\biggr], \\ J&=4M_{02}-R^{2}M_{00}=-4(a-b)\sqrt{R^{2}-t^{2}} \\ &\times\biggl[{\frac{1}{6}}\biggl(pt^{2}-R^{2}p-{\frac{3}{2}}R^{2}t\biggr)+{\frac{1}{4}}R^{2}p\biggr] \end{aligned}\tag{6.9}\]进而,我们有:
\[\begin{aligned} H(2R^{2}-pt-p^{2}) &=M_{10}[3R^{2}t+3R^{2}p-2pt^{2}-2tp^{2}-2p^{3}] \\ J(2R^{2}-pt-p^{2})&=M_{10}[-3R^{2}t+R^{2}p+2pt^{2}] \end{aligned}\tag{6.10}\]将公式 \((6.10)\) 中国两式相加,我们可以得到:
\[(H+J)(2R^2-pt-p^2)=2M_{10}(2R^2-pt-p^2)p\tag{6.11}\]显然 \(2R^2-pt-p^2\neq 0\) ,否则 \(\vert p\vert=\vert t\vert=R\) ,即 \(S\) 中无角点。
然后我们得到了想要的角点坐标 \(p\) :
\[p=\frac{H+J}{2M_{10}}=\frac{2(M_{20}+M_{02})-R^2M_{00}}{M_{10}}\tag{6.12}\]根据 \(O^\prime\) 在原坐标系下的坐标可以得到角点的转换后的坐标为:
\[\begin{aligned}\hat{x}&=x+p\cos\theta\\ \hat{y}&=y+p\sin\theta \end{aligned}\tag{6.13}\]注意其中 \(\cos\theta\) 和 \(\sin\theta\) 可以由公式 \((6.3)\) 给出。
而公式 \((6.12)\) 中代数矩 \(M_{10},M_{00},M_{20},M_{02}\) 可以由公式 \((6.5)\) 从原始的代数矩中导出:
\[\begin{aligned} M_{00}=&(m_{01}^2+m_{10}^2)^{0}\binom{0}{0}\binom{0}{0}(-1)^0m_{10}^0m_{01}^0m_{00}=m_{00}\\ M_{10}=&(m_{01}^2+m_{10}^2)^{-\frac{1}{2}}\biggl\{\binom{1}{0}\binom{0}{0}(-1)^{0}m_{10}m_{01}^{0}m_{10}\\ &+\binom{1}{1}\binom{0}{0}(-1)^{0}m_{10}^{0}m_{01}^{1} m_{01}\biggr\}\\ =&(m_{01}^2+m_{10}^2)^{-\frac{1}{2}}(m_{01}^2+m_{10}^2)\\ =&\sqrt{m_{01}^2+m_{10}^2}\\ M_{01}=&(m_{01}^2+m_{10}^2)^{-\frac{1}{2}}\biggl\{\binom{0}{0}\binom{1}{0}(-1)^{1}m_{10}^{0}m_{01}m_{10}\\ &+\binom{0}{0}\binom{1}{1}(-1)^{0}m_{10}m_{01}^{0} m_{01}\biggr\}\\ =&(m_{01}^2+m_{10}^2)^{-\frac{1}{2}}(-m_{01}^2+m_{10}^2)\\ =&\frac{m_{10}^2-m_{01}^2}{\sqrt{m_{01}^2+m_{10}^2}}\\ M_{20}=&(m_{01}^2+m_{10}^2)^{-1}\biggl\{\binom{2}{0}\binom{0}{0}(-1)^{0}m_{10}^{2}m_{01}^{0} m_{20}\\ &+\binom{2}{1}\binom{0}{0}(-1)^{0}m_{10}^{}m_{01}^{} m_{11}\\ &+\binom{2}{2}\binom{0}{0}(-1)^{0}m_{10}^{0}m_{01}^{2} m_{02}\biggr\}\\ =&(m_{01}^2+m_{10}^2)^{-1}\left(m_{10}^{2}m_{20}+ 2m_{01}m_{10}m_{11}+m_{01}^{2} m_{02}\right)\\ M_{02}=&(m_{01}^2+m_{10}^2)^{-1}\biggl\{\binom{0}{0}\binom{2}{0}(-1)^{2}m_{10}^{0}m_{01}^{2} m_{20}\\ &+\binom{0}{0}\binom{2}{1}(-1)^{1}m_{10}^{}m_{01}^{} m_{11}\\ &+\binom{0}{0}\binom{2}{2}(-1)^{0}m_{10}^{2}m_{01}^{0} m_{02}\biggr\}\\ =&(m_{01}^2+m_{10}^2)^{-1}\left(m_{01}^{2}m_{20}- 2m_{01}m_{10}m_{11}+m_{10}^{2} m_{02}\right) \end{aligned}\tag{6.14}\]其中, \(\binom{m}{n}=\binom{n}{m}=\frac{n!}{m!(n-m)!},n\geq m\) 是组合数。
论文中还给出了 \(t,a,b,\phi\) 的解,同时给出了角点非线性边准则,坐标系中心位置,区域一致性等判准辅助判断角点和角点边,此处一并略去。
6.# Python code
7 SOGDD、FOGDD
7.1 定义
FOGDD和SOGDD17本质是高斯方向导数滤波。
在 \(2D\) 笛卡尔坐标系统中,高斯滤波函数 \(g_\sigma(x,y)\) 可以表示为:
\[g_\sigma(x,y)=\frac{1}{2\pi\sigma^2}\exp\left(-\frac{(x^2+y^2)}{2\sigma^2}\right)\tag{7.1}\]对应地,考虑 \(\theta\) 方向的求导,其一阶方向导数 \(FOGDD\) 和二阶方向导数 \(SOGDD\) 分别表示为:
\[\begin{aligned} \phi_{\sigma,\theta}(x,y) &={\frac{\partial g_{\sigma}}{\partial x}}(\mathbf{R}_{\theta}[x,y]^{\top}) \\ &=-\frac{(x\mathrm{cos}\theta+y\mathrm{sin}\theta)}{\sigma^{2}}g_{\sigma,\theta}(x,y), \\ \psi_{\sigma,\theta}(x,y) &=\frac{\partial^{2}g_{\sigma}}{\partial x^{2}}(\mathbf{R}_{\theta}[x,y]^{\top}) \\ &=\frac{1}{\sigma^2}\left(\frac{1}{\sigma^2}(x\mathrm{cos}\theta+y\mathrm{sin}\theta)^2-1\right)g_{\sigma,\theta}(x,y) \end{aligned}\tag{7.2}\]其中:
\[\mathbf{R}_\theta=\begin{bmatrix}\cos\theta&\sin\theta\\-\sin\theta&\cos\theta\end{bmatrix}\tag{7.3}\]而角点区域可以视作为多个楔形区域 \(\gamma_{\alpha_{i},\alpha_{i+1}}\) 叠加,角点即为这些楔形区域的公共点:
\[\hbar(x,y)=\sum_{i=1}^{r}T_{i}\gamma_{\alpha_{i},\alpha_{i+1}}(x,y)\tag{7.4}\]那么对角点区域用 \(FOGDD\) 和 \(SOGDD\) 执行卷积运算可得:
\[\begin{aligned} \kappa_{\sigma}(\theta) &=\int_{-\infty}^{+\infty}\int_{-\infty}^{+\infty}\hbar(0-x,0-y)\phi_{\sigma,\theta}(x,y)\mathrm{d}x\mathrm{d}y \\ &=\frac{1}{2\sqrt{2\pi}\sigma}\sum_{i=1}^{r}T_{i}\bigg(\cos(\alpha_{i+1}-\theta)-\cos(\alpha_{i}-\theta)\bigg) \\ \varrho_{\sigma}(\theta) &=\int_{-\infty}^{+\infty}\int_{-\infty}^{+\infty}\hbar(0-x,0-y)\psi_{\sigma,\theta}(x,y)\mathrm{d}x\mathrm{d}y \\ &=\frac{1}{2\pi\sigma^{2}}\sum_{i=1}^{r}T_{i}\mathrm{sin}(\alpha_{i}+\alpha_{i+1}-2\theta)\mathrm{sin}(\alpha_{i+1}-\alpha_{i}) \end{aligned}\tag{7.5}\]考虑到卷积的一个性质:
\[\left(\left(f(\tau)*g(\tau)\right)(t)\right)^{\prime}=\left(f(\tau)*g^{\prime}(\tau)\right)(t)\tag{7.6}\]式 \((7.5)\) 本质可以看作先对图像区域在 \(\theta\) 方向求导再高斯滤波。
将上述公式在离散空域内表达为:
\[\begin{aligned} &&g_{\sigma}(\mathbf{n})& ={\frac{1}{2\pi\sigma^{2}}}\exp\left(-{\frac{1}{2\sigma^{2}}}\mathbf{n}^{\top}\mathbf{n}\right), \\ &&\phi_{\sigma,k}(\mathbf{n})& =-\frac{([\mathrm{cos}\theta_{k}\mathrm{sin}\theta_{k}]\mathbf{n})}{\sigma^{2}}g_{\sigma}(\mathbf{n}), \\ &&\psi_{\sigma,k}(\mathbf{n})& =\frac{1}{\sigma^{2}}\left(\frac{1}{\sigma^{2}}([\mathrm{cos}\theta_{k}~\mathrm{sin}\theta_{k}]\mathbf{n})^{2}-1\right)g_{\sigma}(\mathbf{n}), \\ &&\mathbf{R}_{k}& =\begin{bmatrix}\cos\theta_k&\sin\theta_k\\-\sin\theta_k&\cos\theta_k\end{bmatrix},\mathbf{n}=\begin{bmatrix}n_x\\n_y\end{bmatrix}\in\mathbb{Z}^2 \end{aligned}\tag{7.7}\]类似地,对图像区域做卷积:
\[\begin{aligned} \delta_{\sigma,k}(\mathbf{n})& =\sum_{m_{x}}\sum_{m_{y}}I(\mathbf{n}-\mathbf{m})\phi_{\sigma,k}(\mathbf{m}), \\ \ell_{\sigma,k}(\mathbf{n})& =\sum_{m_{x}}\sum_{m_{y}}I(\mathbf{n}-\mathbf{m})\psi_{\sigma,k}(\mathbf{m}), \\ \text{m}& =[m_{x},m_{y}]^{\top}\in\mathbb{Z}^{2} \end{aligned}\tag{7.8}\]为了更好地区分角点、边缘点和斑点,对 \((7.8)\) 中的公式进一步处理为:
\[\xi_{\sigma,k}(n_{x},n_{y})=\mid\delta_{\sigma,k}(n_{x},n_{y})\mid\times\mid\ell_{\sigma,k}(n_{x},n_{y})\mid \tag{7.9}\]在一个大小为 \((p+1)\times(q+1)\) 的图像块内,计算得到如下矩阵,
\[\begin{aligned}&\Lambda_{\sigma_c}(n_x,n_y)=\\&\begin{bmatrix}\sum_{i=-\frac{n}{2}}^{\frac{p}{2}}\sum_{j=-\frac{q}{2}}^{\frac{q}{2}}\xi_{\sigma_{x,1}}^2(n_x+i,n_y+j)&\cdots&\sum_{i=-\frac{p}{2}}^{\frac{p}{2}}\sum_{j=-\frac{q}{2}}^{\frac{q}{2}}\xi_{\sigma_x+i,n_y+j})\xi_{\sigma_{x,K}}(n_x+i,n_y+j)\\\vdots&\ddots&\vdots\\\sum_{i=-\frac{k}{2}}^{\frac{p}{2}}\sum_{j=-\frac{4}{2}}^{\frac{q}{2}}\xi_{\sigma_{x,K}}(n_x+i,n_y+j)\xi_{\sigma_{x,1}}(n_x+i,n_y+j)&\cdots&\sum_{i=-\frac{k}{2}}^{\frac{p}{2}}\sum_{j=-\frac{4}{2}}^{\frac{q}{2}}\xi_{\sigma_{x,K}}^2(n_x+i,n_y+j)\end{bmatrix}\end{aligned}\tag{7.10}\]依据其特征值得到判别函数: \(\Upsilon_e(n_x,n_y)=\frac{\prod_{k=1}^K\lambda_k}{\sum_{k=1}^K\lambda_k+\varsigma}\tag{7.11}\)
$\Upsilon_e$ 是局部极大值且大于一个阈值 $T_c$ 时即视为角点。
7.2 理论溯源
早在1991年William T. Freeman的IEEE论文The Design and Use of Steerable Filters中即给出了名为方向可调滤波(steerable filter)的定义18:
\[G_{\hat{\mathbf{u}}}=uG_x+vG_y=u\frac{\partial G}{\partial x}+v\frac{\partial G}{\partial y}\tag{7.12}\]式中, $\hat{\mathbf{u}}=[cos \theta,sin \theta]^\top=[u,v]^\top$ 为 $\theta$ 方向上的单位向量,代入后不难发现其与公式 $(7.2)$ 中的一阶高斯方向导数 $FOGDD$ 完全相同,也即 $\phi_{\sigma,\theta}(x,y)=G_{\hat{\mathbf{u}}}$ 。相应地,对标公式 $(7.5)$ 也有:
\[\kappa_{\sigma}(\theta)=\mathbf{\hat{u}}\cdot\nabla(G*f)=\nabla_{\mathbf{\hat{u}}}(G*f)=(\nabla_{\mathbf{\hat{u}}}G)*f\tag{7.13}\]而二阶高斯方向导数 $SOGDD$ 则可定义为:
\[G_{\hat{\mathbf{u}}\hat{\mathbf{u}}}=u^2G_{xx}+2uvG_{xy}+v^2G_{yy}\tag{7.14}\]8 SuperPoint
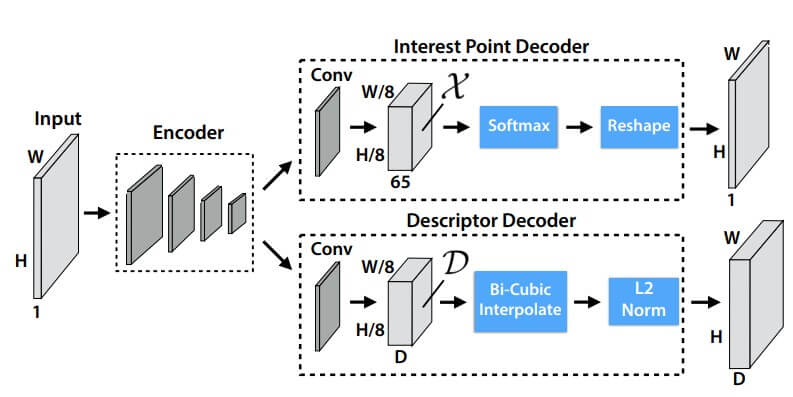
SuperPoint19利用由点线面等基本几何要素构成的虚拟数据集进行训练得到伪真值,辅以多样射影变换以提升前者提取的所谓MagicPoint的普适性,以此替代人工标注的过程。这里不对原理做赘述,SuperPoint的网络架构如下图所示:
接下来我们重点探讨怎么将官方的预训练模型20在C++中进行调用。有多种推理框架,我们这里以OpenCV的DNN模块为例。首先需要将官方的pth权重文件转换为onnx格式21,接下来就是读取这个onnx文件,进行模型推理,根据论文以及官方python代码从推理结果中提取角点特征。
一张灰度图经过推理后会生成两个张量,注意这个张量相比原图在长和宽的大小上变成了原本的1/8,这一点会体现在坐标的转换上。然后就是很常规的置信度阈值提取角点坐标,双线性内插获取角点描述子,具体的C++代码如下所示,其中SuperPoint_Impl是SuperPoint的实现类,cv::Feature2D的子类。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
void cv::SuperPoint_Impl::detectAndCompute(InputArray _image, InputArray _mask, std::vector<KeyPoint>& keypoints,
OutputArray _descriptors, bool use_provided_keypoints)
{
// 0.prepare
bool do_keypoints = !use_provided_keypoints;
bool do_descriptors = _descriptors.needed();
cv::Mat image = _image.getMat(), mask = _mask.getMat();
if (image.type() != CV_8UC1)
{
cv::cvtColor(image, image, COLOR_BGR2GRAY);
}
if (image.rows % 8 != 0)
{
size_t row_border = 8 - image.rows % 8;
size_t col_border = 0;
if (image.cols % 8 != 0)
{
col_border = 8 - image.cols % 8;
}
cv::copyMakeBorder(image, image, 0, row_border, 0, col_border, cv::BORDER_CONSTANT, cv::Scalar::all(0));
}
// 1.model inference
cv::dnn::Net model = dnn::readNetFromONNX(onnx_file);
if (model.empty())
{
CV_Error(Error::StsError, "The onnx file is invalid!");
return;
}
if (use_cuda)
{
CV_Assert(cv::cuda::getCudaEnabledDeviceCount() > 0);
model.setPreferableBackend(cv::dnn::Backend::DNN_BACKEND_CUDA);
model.setPreferableTarget(cv::dnn::Target::DNN_TARGET_CUDA);
}
cv::Mat blob;
cv::dnn::blobFromImage(image, blob, 1 / 255.0);
model.setInput(blob);
std::vector<Mat> output_blobs;
model.forward(output_blobs, model.getUnconnectedOutLayersNames());
// 2.extract keypoints
if (do_keypoints)
{
keypoints.clear();
int reserve_size = 2 * image.total() / 64;
keypoints.reserve(reserve_size);
cv::MatSize semi_points_size = output_blobs[1].size;
cv::Mat semi_points, confidence;
cv::transposeND(output_blobs[1], { 0, 2, 3, 1 }, semi_points);
semi_points = semi_points.reshape(65, { semi_points_size[2], semi_points_size[3] });
cv::exp(semi_points, confidence); // softmax
const cv::Vec<float, 65> ones_vec = cv::Vec<float, 65>::ones();
auto _confidence_threshold_functor = [&keypoints, &ones_vec, this](cv::Vec<float, 65> &pixel, const int *position) -> void
{
std::lock_guard<std::mutex> locker(mutex_);
float cell_sum = pixel.dot(ones_vec);
for (int k = 0; k < 64; k++)
{
float candidate_confidence = pixel[k] / (cell_sum + (float)1e-5);
if (candidate_confidence > confidence_threshold)
{
cv::Point corner = cv::Point(position[1] * 8 + k % 8, position[0] * 8 + k / 8);
keypoints.push_back(KeyPoint(corner, 7.f, -1, candidate_confidence));
}
}
};
confidence.forEach<cv::Vec<float, 65>>(_confidence_threshold_functor);
// Remove keypoints out of mask region
cv::KeyPointsFilter::runByPixelsMask(keypoints, mask);
// Remove keypoints very close to the border
cv::KeyPointsFilter::runByImageBorder(keypoints, image.size(), edge_threshold);
// Nonmax suppression
runByFastNonmaxSuppression(keypoints, image.size(), nonmax_suppression_size);
}
// 3.extract descriptors
if (do_descriptors)
{
int keypoints_num = keypoints.size();
if (keypoints_num == 0)
{
_descriptors.release();
return;
}
_descriptors.create(keypoints_num, DESCRIPTOR_SIZE, CV_32F); // Nx256
cv::Mat descriptors_mat = _descriptors.getMat();
cv::Mat semi_dense_descriptors;
cv::MatSize semi_descriptors_size = output_blobs[0].size;
semi_dense_descriptors = output_blobs[0].reshape(0, { semi_descriptors_size[1], semi_descriptors_size[2], semi_descriptors_size[3] });
// Interpolate
cv::parallel_for_(Range(0, keypoints_num), [&semi_dense_descriptors = std::as_const(semi_dense_descriptors), &keypoints, &descriptors_mat](const Range &range)
{
for (int n = range.start; n < range.end; n++)
{
auto pt = keypoints[n].pt;
float i = pt.y / 8.;
float j = pt.x / 8.;
// bilinear interpolation
const int neighbor_grid[4] = { floor(j - (float)1e-5), ceil(i), ceil(j), floor(i - (float)1e-5) };
const float w[4] = { j - neighbor_grid[0], neighbor_grid[1] - i, neighbor_grid[2] - j, i - neighbor_grid[3] };
float norm_factor = 0.;
for (int k = 0; k < DESCRIPTOR_SIZE; k++)
{
uchar *p_desc = semi_dense_descriptors.data + k * semi_dense_descriptors.step.p[0]
+ neighbor_grid[3] * semi_dense_descriptors.step.p[1]
+ neighbor_grid[0] * semi_dense_descriptors.step.p[2];
float el = w[1] * w[2] * (*(float*)p_desc)
+ w[2] * w[3] * (*(float*)(p_desc + semi_dense_descriptors.step.p[1]))
+ w[0] * w[3] * (*(float*)(p_desc + semi_dense_descriptors.step.p[1] + semi_dense_descriptors.step.p[2]))
+ w[0] * w[1] * (*(float*)(p_desc + semi_dense_descriptors.step.p[2]));
norm_factor += el * el;
(*descriptors_mat.ptr<float>(n, k)) = el;
}
for (int k = 0; k < DESCRIPTOR_SIZE; k++)
{
(*descriptors_mat.ptr<float>(n, k)) /= sqrt(norm_factor) + 1e-5;
}
}
});
}
}
展开
参考
Harris C G , Stephens M J .A combined corner and edge detector[C]//Alvey vision conference.1988. https://doi.org/10.5244/C.2.23 ↩︎
drawing-ellipse-from-eigenvalue-eigenvector https://math.stackexchange.com/questions/1447730/drawing-ellipse-from-eigenvalue-eigenvector ↩︎
Rosten E .Machine learning for high-speed corner detection[C]//European Conference on Computer Vision.Springer-Verlag, 2006. https://doi.org/10.1007/11744023_34 ↩︎
ID3 Algorithm https://en.wikipedia.org/wiki/ID3_algorithm ↩︎
Information Gain https://en.wikipedia.org/wiki/Information_gain_(decision_tree) ↩︎
Mair E , Hager G D , Burschka D ,et al.Adaptive and Generic Corner Detection Based on the Accelerated Segment Test[C]//ECCV 2010;European conference on computer vision.2010. https://link.springer.com/chapter/10.1007/978-3-642-15552-9_14 ↩︎
what-is-phase-congruency https://dsp.stackexchange.com/questions/22700/what-is-phase-congruency ↩︎
Kovesi P .Phase Congruency Detects Corners and Edges[C]//Dicta.2003 https://www.peterkovesi.com/papers/phasecorners.pdf ↩︎
Kovesi P .Image Features From Phase Congruency[J].The University of Western Australia, 1995(3). https://www.semanticscholar.org/paper/Image-Features-from-Phase-Congruency-Kovesi/4d954ec7f1091cb1d6b18b1b1e656d583e7a1353 ↩︎
An implementation of phase congruency image features detection: edges and corners. https://github.com/RamilKadyrov/PhaseCongruency ↩︎
Mokhtarian F , Suomela R .Robust image corner detection through curvature scale space[J].IEEE Computer Society, 1998(12). https://link.springer.com/chapter/10.1007/978-94-017-0343-7_7 ↩︎
Awrangjeb M , Lu G .Robust Image Corner Detection Based on the Chord-to-Point Distance Accumulation Technique[J].IEEE Transactions on Multimedia, 2008, 10(6):1059-1072.DOI:10.1109/TMM.2008.2001384. https://www.semanticscholar.org/paper/Robust-Image-Corner-Detection-Based-on-the-Distance-Awrangjeb-Lu/3add640b10af15eb3272abfa95e62bb522ac175d ↩︎
ARCSS corner detector https://www.mathworks.com/matlabcentral/fileexchange/33229-affine-resilient-curvature-scale-space-corner-detector ↩︎
CPDA corner detector https://www.mathworks.com/matlabcentral/fileexchange/22390-robust-image-corner-detection-based-on-the-chord-to-point-distance-accumulation-technique?s_tid=srchtitle ↩︎
Abramenko A A, Karkishchenko A N. 2019. Applications of Algebraic Moments for Corner and Edge Detection for a Locally Angular Model[J/OL]. Pattern Recognition and Image Analysis, 29(1): 58-71. https://doi.org/10.1134/S1054661819010024 ↩︎
GitHub. mr-abramenko/subpixel-corner-edge-detector: Subpixel corner and edge detector. https://github.com/mr-abramenko/subpixel-corner-edge-detector ↩︎
Zhang W, Sun C, Gao Y. 2023. Image Intensity Variation Information for Interest Point Detection[J/OL]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 45(8): 9883-9894. https://doi.org/10.1109/TPAMI.2023.3240129 ↩︎
Szeliski_Computer Vision Algorithms and Applications_2ndEd.Charpter3.2.3 page127-129 https://szeliski.org/Book ↩︎
Detone D, Malisiewicz T, Rabinovich A. SuperPoint: Self-Supervised Interest Point Detection and Description[J]. 2017. https://doi.org/10.48550/arXiv.1712.07629 ↩︎
SuperPoint Weights File and Demo Script. https://github.com/magicleap/SuperPointPretrainedNetwork ↩︎
将PyTorch训练模型转换为ONNX. https://learn.microsoft.com/zh-cn/windows/ai/windows-ml/tutorials/pytorch-convert-model ↩︎